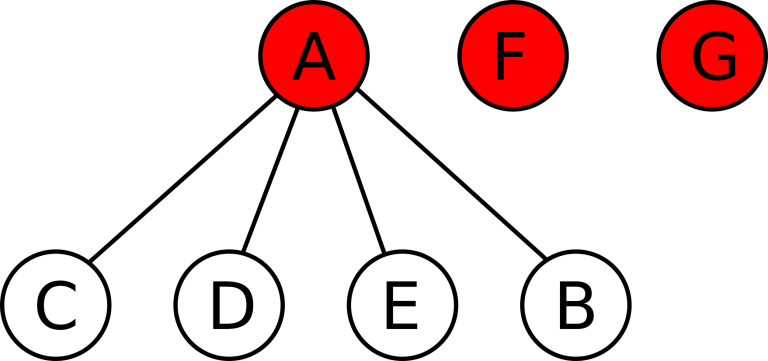
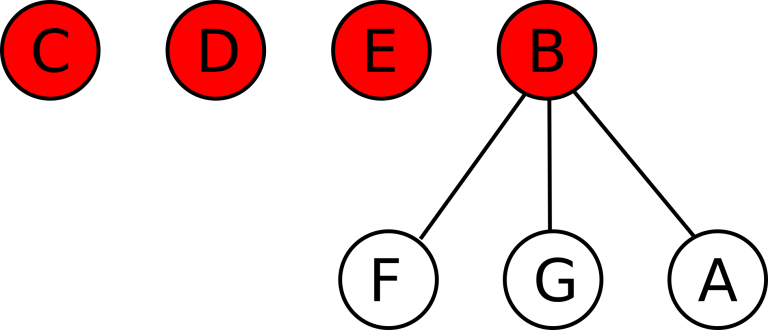
有 n n n
以下过程会一直进行,直到只剩下一个活跃的公司。每次执行下列步骤需要恰好 1 天:
随机等概率选出两个不同的活跃公司 A A A B B B 掷一次公平的硬币,等概率地决定 A A A B B B B B B A A A A A A B B B B B B A A A 当一个公司从活跃变为已被收购时,它之前所有已被收购的下属公司都会变为活跃状态。 例如,可能出现如下情形:假设 A A A B B B C C C D D D E E E A A A F F F G G G B B B
如果 A A A B B B A A A F F F G G G C C C D D D E E E B B B A A A F F F G G G
如果反过来 B B B A A A B B B C C C D D D E E E F F F G G G A A A B B B C C C D D D E E E
现在给定初创公司的初始状态。对于每个公司,告知其是活跃还是已被收购。如果是已被收购,还会给出它当前跟随的活跃公司的编号。
你需要计算,最终只剩下一个活跃公司时,所需天数的期望值。
可以证明,期望天数可以表示为有理数 P / Q P/Q P / Q P P P Q Q Q Q ≠ 0 ( m o d 1 0 9 + 7 ) Q \not= 0 \pmod{10^9+7} Q = 0 ( m o d 1 0 9 + 7 ) P ⋅ Q − 1 P \cdot Q^{-1} P ⋅ Q − 1 1 0 9 + 7 10^9+7 1 0 9 + 7
对于这类比较复杂的操作,问期望时间的问题有个技巧是用鞅与停时定理做。
具体地,设 f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) f f f 1 1 1
这题我们设 a i a_i a i i i i ∑ f ( a i ) \sum f(a_i) ∑ f ( a i )
Δ = 1 m ( m − 1 ) ∑ i = 1 m ∑ j ≠ i [ f ( a i + 1 ) + ( a j − 1 ) f ( 1 ) − f ( a i ) − f ( a j ) ] = 1 m ∑ i = 1 m [ f ( a i + 1 ) + ( a i − 1 ) f ( 1 ) − 2 f ( a i ) ] = − 1 \begin{aligned} \Delta=&\frac{1}{m(m-1)}\sum_{i=1}^{m}{\sum_{j\neq i}}{\left[f(a_i+1)+(a_j-1)f(1)-f(a_i)-f(a_j)\right]}\\ =&\frac{1}{m}\sum_{i=1}^{m}{\left[f(a_i+1)+(a_i-1)f(1)-2f(a_i)\right]}=-1\\ \end{aligned} Δ = = m ( m − 1 ) 1 i = 1 ∑ m j = i ∑ [ f ( a i + 1 ) + ( a j − 1 ) f ( 1 ) − f ( a i ) − f ( a j ) ] m 1 i = 1 ∑ m [ f ( a i + 1 ) + ( a i − 1 ) f ( 1 ) − 2 f ( a i ) ] = − 1
由于我们可以随意确定 f ( x ) f(x) f ( x ) f ( 1 ) = 0 f(1)=0 f ( 1 ) = 0 f ( a i + 1 ) − 2 f ( a i ) f(a_i+1)-2f(a_i) f ( a i + 1 ) − 2 f ( a i ) − 1 -1 − 1 f ( x ) = 2 f ( x − 1 ) − 1 f(x)=2f(x-1)-1 f ( x ) = 2 f ( x − 1 ) − 1 f ( 1 ) = 0 f(1)=0 f ( 1 ) = 0 f ( x ) = 1 − 2 x − 1 f(x)=1-2^{x-1} f ( x ) = 1 − 2 x − 1
最终答案为 ∑ f ( a i ) − f ( n ) \sum f(a_i)-f(n) ∑ f ( a i ) − f ( n ) a i a_i a i i i i
时间复杂度:O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> const int kMaxN = 505 , kMod = 1e9 + 7 ;int n;int cnt[kMaxN];int qpow (int bs, int64_t idx = kMod - 2 ) int ret = 1 ;for (; idx; idx >>= 1 , bs = (int64_t )bs * bs % kMod)if (idx & 1 )int64_t )ret * bs % kMod;return ret;inline int add (int x, int y) return (x + y >= kMod ? x + y - kMod : x + y); }inline int sub (int x, int y) return (x >= y ? x - y : x - y + kMod); }inline void inc (int &x, int y) inline void dec (int &x, int y) 0 ? x += kMod : x; }void dickdreamer () for (int i = 1 ; i <= n; ++i) {int x;if (x == -1 ) ++cnt[i];else ++cnt[x];int ans = 0 ;for (int i = 1 ; i <= n; ++i)if (cnt[i])inc (ans, sub (1 , qpow (2 , cnt[i] - 1 )));dec (ans, sub (1 , qpow (2 , n - 1 )));'\n' ;int32_t main () #ifdef ORZXKR freopen ("in.txt" , "r" , stdin);freopen ("out.txt" , "w" , stdout);#endif sync_with_stdio (0 ), std::cin.tie (0 ), std::cout.tie (0 );int T = 1 ;while (T--) dickdreamer ();return 0 ;