模拟费用流学习笔记
首先模拟费用流有两种不同的方法:
如果不要求动态加入或者删除,只需要求全局的费用流或者流量小于等于某个数的费用流,可以用 EK 增广的方法,每次选当前图上费用最优的增广路增广。
如果要求动态加入并且只要求费用最优,可以每次选择费用最小的源汇路径或者一个经过新加的点的费用最小的负环进行增广。
注:EK 增广的时候一定不会出现环,并且第一个方法与源点或者汇点相连的边也一定不会发生退流。
P4694 [PA 2013] Raper
Description
你需要生产 张光盘。每张光盘都要经过两道工序:先在 A 工厂进行挤压,再送到 B 工厂涂上反光层。
Solution
考虑费用流,先建图:
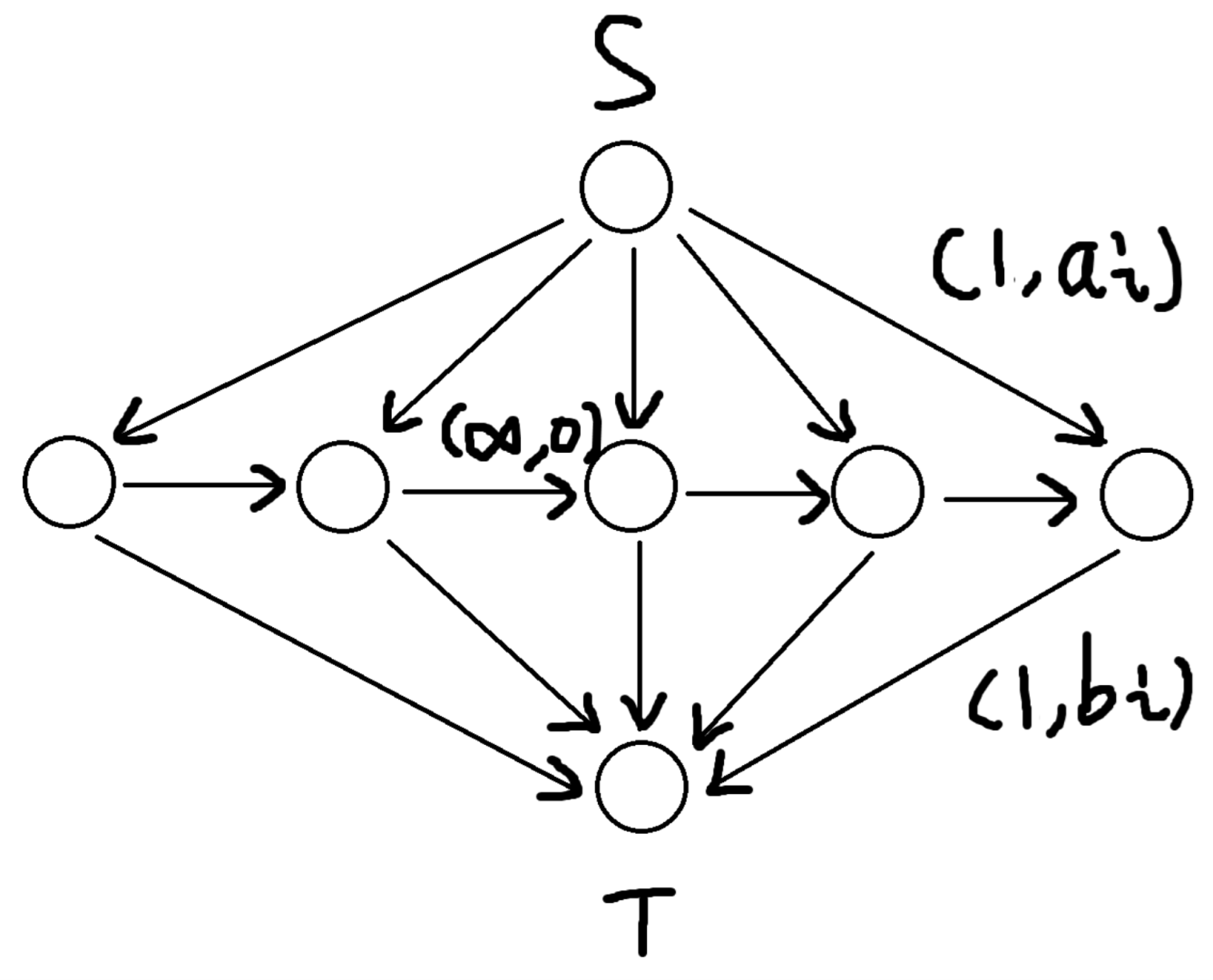
考虑用第一种方法直接 EK 增广。
首先是从左往右,这个相当于是选择没被选的 和 进行匹配,并让 的这些中间边反向边流量加一。
然后是从右往左,此时是选择没被选的 和 并且 中间反向边流量不小于 的 和 进行匹配,并且这些反向边流量减一。
用线段树维护中间的反向边流量和没被删掉的 与 即可。
时间复杂度:。
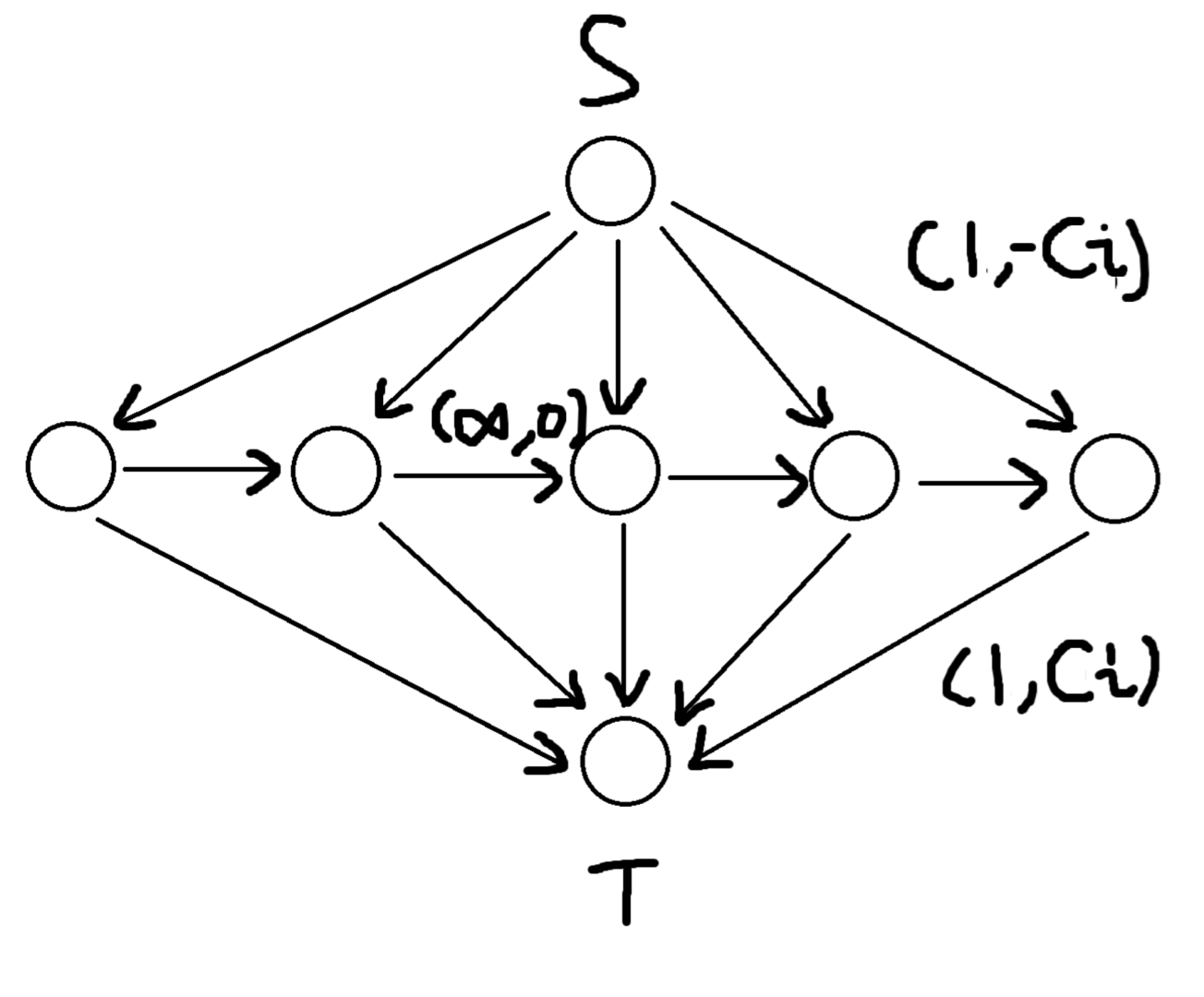
CF865D Buy Low Sell High
Description
已知接下来 天的股票价格 ,每天你可以买进一股股票,卖出一股股票,或者什么也不做。
假设你拥有无限本金,求 天之后能得到的最大利润。
Solution
和上面那题是一样的。
P6122 [NEERC 2016] Mole Tunnels
Description
给出一棵 个点的树,编号为 ,以 为根。节点 的父亲为 。
第 个洞内有 个食物,共有 只鼹鼠,第 只住在点 。
对于所有 ,前 只鼹鼠各找到一个食物,在树上行走的最小总距离。
Solution
首先还是建出费用流模型。
由于这里要动态加点,所以要用方法 2。但是注意到跑负环是不优的,因为这里要求最大流,由于负环是让新来的鼹鼠替代某个原来的鼹鼠进行匹配,然后原来的鼹鼠重新匹配。这不如直接跑源汇路径进行反悔。于是直接维护当前点能到的所有点即可。
由于树高只有 ,所以可以暴力修改。
时间复杂度:。
P9168 [省选联考 2023] 人员调度
Description
Solution
这题还是先建出费用流模型,和上题差不多,但是只有往儿子的正向边。
首先可以用线段树分治把删除转化成添加。然后同样地去讨论是源汇路径还是走负环。
这两个分别代表走初始位置到根的路径上的反向边到达最高点,再从子树里选择一个没有被选过的点进行匹配;或者往根走反向边,并选择一个人替换成当前人。
这两个可以用树链剖分维护,时间复杂度:。
总的时间复杂度:。