前言
卡特兰数是初赛中比较重要的数学知识,所以写篇博客总结一下。
定义
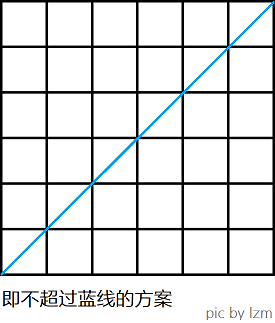
用 Cn 表示从 (0,0) 出发,每次只能向右或向上走 1 步,且 x 轴的值始终不小于 y 轴的值,到 (n,n)的方案种数。
通项+证明
Cn=n+11(2nn)
证明:

不考虑越过线的情况的话显然有 (2nn) 种情况。
考虑非法的情况,令直线 l:y=x+1,那么每一个非法的方案都与 l 有至少 1 个交点。
对于每一个方案,我们取 x 值最小且在 l 上的点记为 p(x1,y1),将 x>x1,y≤x 的点沿 l 对称,那么就变为从 (0,0) 到 (n−1,n+1) 的路径了,显然是一个映射,所以有 (2nn−1) 种非法方案。
所以 Cn=(2nn)−(2nn−1)。
化简
Cn====(2nn)−(2nn−1)n!⋅n!(2n)!−(n−1)!⋅(n+1)!(2n)!(2n)!⋅[n!⋅(n+1)!(n+1)−n]n+11(2nn)
应用
- n 对括号的合法配对方案书
- n 个节点的二叉树的形态数
- n+1 个叶子(n 个非叶节点)的满二叉树的形态数, 走到左儿子 +1,走到 右儿子 −1,类似于括号匹配(大致同2)
- n 个数入栈后出栈的排列总数
- 对凸 n+2 边形进行不同的三角形分割的方案数(分割线断点仅为顶点,且分割线仅在顶点上相交)
- n 层的阶梯切割为 n 个矩形的切法数
转自 https://www.cnblogs.com/linzhengmin/p/11298140.html。

